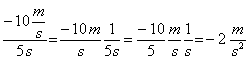COLABORACIONES

Kilómetro por hora, años-persona, ji cuadrado: temas dimensionales, métricos y algebraicos en la redacción y traducción de textos científicos

Para M. L. B.

Dice Jesús Mosterín que la profusa variedad de conceptos científicos se puede reducir a tres tipos de conceptos: clasificatorios, comparativos y métricos. Los conceptos clasificatorios vienen dados por los sustantivos y adjetivos del lenguaje ordinario y corresponden a lo cualitativo, mientras que los conceptos métricos corresponden a lo cuantitativo y los conceptos comparativos o topológicos a un tipo intermedio. Ahora bien, según Mosterín, «los conceptos métricos, también llamados conceptos cuantitativos o magnitudes, no tienen correspondencia en el lenguaje ordinario. Son una creación original del lenguaje científico». Quizá sea esa la razón por la que algunas personas con muy buena capacidad verbal tienen enormes dificultades con lo cuantitativo y temen a las matemáticas y a los números como a una especie de misterio.

Este trabajo explica algunos aspectos básicos relativos a las magnitudes de uso habitual en la vida cotidiana y en todos los campos de las ciencias naturales y sociales. Me decidí a escribirlo tras comprobar por diversas lecturas y discusiones que muchas personas cultas tienen ideas imprecisas o abiertamente equivocadas sobre estos temas, lo que a mi juicio es fruto casi siempre de la falta de familiaridad con los conceptos básicos de la teoría de la medición, el análisis dimensional y el álgebra. Pero esos campos se refieren a aspectos muy generales conectados con todas las ciencias básicas y aplicadas y en la redacción, edición y traducción de textos científicos surgen continuamente problemas relacionados con estos ámbitos. Así, por ejemplo, para traducir correctamente del inglés al castellano una frase como pooled person-time added up to 988.0 woman-years, aunque sea inconscientemente habrá que resolver problemas de teoría de la medición y de análisis dimensional (más adelante volveré a esta frase). Todos los implicados en la labor científica o en la labor editorial o de traducción de textos científicos deberían conocer al menos los fundamentos de la teoría métrica y del análisis dimensional.

Un físico español que contribuyó considerablemente al desarrollo del análisis dimensional fue Julio Palacios, que fue miembro de la Real Academia Española, Presidente de la Real Academia de Ciencias Exactas, Físicas y Naturales y, también, autor del libro Análisis dimensional, obra que tuvo suficiente repercusión en el mundo científico como para que fuera traducida al inglés y publicada en 1964 por la editorial británica Macmillan (lamentablemente, para preparar este texto solo he tenido a mi alcance esa versión traducida y no la versión original en castellano). Que Julio Palacios se preocupaba por las cuestiones de terminología y traducción queda claro, por ejemplo, por los comentarios sobre correspondencias inglés-español que aparecen en el prefacio a la edición inglesa de su libro:

To achieve a good English translation has proved to be a difficult task. One of the problems has been to find the proper words for the Spanish terms magnitud (abstract concept) and cantidad (each of the particular states of a magnitud). At first sight, one would think that these words ought to be translated by 'magnitude' and 'quantity' respectively, but it seems that they have the transposed meaning, because magnitude has in English the same meaning as 'amount' which would be translated in Spanish by cantidad, whilst the Spanish version of the phrase [...] 'dimensions of physical quantities' would be 'dimensiones de las magnitudes físicas'.

On the other hand, one finds in the books that to the statement:

cantidad = medida x  unidad

corresponds:

quantity = measure x unit

which shows that in this case 'quantity' is the English word for cantidad. Hence, the term 'quantity' is used in both senses.

[...] I have discussed this subject with some English physicists and we have decided to use 'quantity' for magnitud and 'amount' for cantidad. Of course, this must be considered as a provisional compromise which may serve as a first step towards a better solution.

Como tantas veces ocurre en asuntos de traducción y terminología, ni las soluciones de un autor son tenidas en cuenta por otros ni se resuelven los problemas de ambigüedad y falta de precisión terminológica. Actualmente ni en castellano ni en inglés hay definiciones claras del significado científico exacto de términos como «cantidad», «magnitud», quantity, magnitud o amount. Para evitar las ambigüedades, cuando más adelante presente ciertos conceptos básicos del análisis dimensional, daré algunas definiciones operativas.

Times, per, by y for, cuatro preposiciones inglesas para el «por» castellano

Bentham decía que nunca es tan difícil destruir el error como cuando este tiene sus raíces en el lenguaje. A menudo las disonancias entre el habla o incluso la lengua escrita y los formalismos matemáticos plasmados en fórmulas y ecuaciones embarullan el análisis de los conceptos científicos. En el mundo de habla hispana un factor que contribuye a crear confusión en las cuestiones dimensionales es el significado, consagrado por millones de usos coloquiales y técnicos -y, en ese sentido, imposible de evitar-, de la preposición «por» para indicar dos operaciones matemáticas exactamente contrarias, la multiplicación (o producto) y la división. Así, cuando decimos cuatro por siete, veintiocho ( 4 x 7 = 28), o que una mesa tiene una superficie de dos metros por tres metros, estamos indicando multiplicaciones (2 m x 3 m, o sea, 6 m²). Por el contrario, cuando decimos que en una escuela hay 300 alumnos y 20 maestros y por tanto hay 15 alumnos por (cada) maestro (15 alumnos/maestro), ese por expresa una división. Igualmente expresan división el por de «120 kilómetros por hora» con el que indicamos una velocidad, o el de «2,3 casos por 1.000 personas», que se refiere a la frecuencia de una enfermedad en una población. Que este por que expresa división da lugar a confusión más de una vez resulta evidente cuando se ve por ejemplo expresada la frecuencia de una enfermedad en «casos x 1.000», o una tasa de mortalidad en «defunciones x 100.000», lo cual es claramente incorrecto (lo correcto sería «casos/1.000» o «defunciones/100.000»).

La ambigüedad matemática de las denotaciones de por en español no tiene una correspondencia clara en inglés, donde los dos significados matemáticos de nuestro «por» corresponden a times (para la multiplicación) y per (para la división). Así «dos por cuatro, ocho» es two times four is eight, mientras que «milla por hora» es mile per hour y casos por millón es cases per million.

Sin embargo, en inglés también existen las preposiciones by y for, que pueden verterse como «por» al castellano, y que a menudo dan lugar a problemas. En frases como a room 7 feet by 10 feet el by inglés indica multiplicación, y «multiplicar por» sería en inglés to multiply by. Pero «dividir por» es en inglés to divide by y así podemos decir por ejemplo, 6x² divided by 3x is 2x. De esta forma la ambigüedad matemática del por en castellano encuentra cierto paralelismo en los usos del by inglés. Por si fueran pocas esas ambigüedades, hay una confusión entre el by y el for que muchas veces da lugar a error en traducciones al español hechas por personas que no saben mucho inglés. Así, por ejemplo, en la jerga de los economistas to substitute capital for labor significa «sustituir trabajo por capital», mientras que to substitute labor for capital significa lo mismo que to substitute capital by labor, es decir, exactamente lo contrario, «sustituir capital por trabajo». Igualmente, to replace aspirin for morphine significa sustituir la morfina por aspirina, mientras que to replace aspirin by morphine es sustituir la aspirina por morfina. En traducciones al español de textos en inglés no es infrecuente encontrar frases mal traducidas en las que, por ejemplo, se habla de sustituir máquinas por mano de obra cuando lo que decía el original inglés, substitute machinery for labor power, era exactamente lo contrario.

Cantidades, unidades y precisión de la medición

Las cantidades que se manejan habitualmente en la vida cotidiana y en las ciencias naturales o sociales suelen ser de dos tipos, recuentos y mediciones (en inglés counts y measurements, respectivamente). Los recuentos son resultado de contar las unidades naturales de algo (en jerga matemática, expresan la cardinalidad de un conjunto) y, forzosamente, son un número natural, es decir, un entero positivo. Ejemplos de recuentos son la población de una villa, el número de tonterías que dice una persona en una conversación (suponiendo que no pueda decirse ni media tontería ni un tercio de tontería), el número total de orejas de los estudiantes de una clase, el aforo de un teatro (o sea, el total de asientos) o los automóviles salidos de una fábrica en un año. Las mediciones o medidas son en cambio el resultado de comparar una magnitud con una unidad arbitraria llamada unidad métrica o unidad de medición o medida. El resultado de dicha comparación indica cuántas veces está contenida la cantidad medida en la unidad de medición. El resultado de la medición depende así no solo de la unidad de medida, sino de la precisión con la que estimemos la magnitud. La altura de una persona puede medirse en metros, en centímetros, en milimicras o en pulgadas y así la estatura de Fulano puede expresarse como 1,8 m, o bien 180 cm. Según la teoría de la medición, si esas medidas están adecuadamente expresadas, al decir que Fulano mide 1,8 m, lo que realmente indicamos es que fue medido con un dispositivo métrico cuya exactitud llegaba a la décima de metro y que la altura medida fue más cercana a la marca de 1,8 que a las de 1,7 o 1,9. Por lo tanto, su altura estaba en un intervalo entre 1,75 m y 1,85 m. En cambio, si la estatura se expresa como 180 cm, lo que realmente se indica es que el resultado de la medición estuvo entre 179,5 cm y 180,5 cm. Así, a pesar de que estaturas expresadas como 1,8 m o como 180 cm son aparentemente lo mismo, realmente la medida expresada en centímetros refleja una estimación estatural mucho más precisa. De lo dicho se deduce inmediatamente que 1,80 m sí es equivalente a 180 cm. Por lo tanto, si las cifras están utilizadas correctamente, el cero después de la coma decimal en «1,80 m» tiene una función métrica importante y no debe eliminarse sin más, como hacen a veces editores, redactores o traductores que no están al tanto de estos asuntos.

Contar y medir

Los físicos denominan magnitud a una propiedad física que puede medirse. El resultado de la medición de una magnitud, dado por un número y una unidad, es una cantidad. Tanto las cantidades como los recuentos tienen unidades. Así, si medimos una distancia, las unidades serán kilómetros, yardas o leguas; la capacidad de una cuba será una cantidad en litros, galones, fanegas o metros cúbicos; la temperatura de un paciente vendrá expresada en grados Celsius o centígrados en la mayor parte de los países, pero serán grados Fahrenheit en Nueva York o en Chicago. En cambio, si contamos las partículas de la corteza atómica tendremos un recuento de electrones, si contamos una piara, las unidades serán cerdos; si contamos el contenido de una canasta de frutas, las unidades serán naranjas, manzanas… lo que corresponda. Como ya se dijo, las unidades en las que se expresa un recuento están dadas por la naturaleza misma de lo que se cuenta. Claro que al contar se abstraen las características concretas de las unidades contadas y si contamos un racimo de uvas y el resultado es 25, en esas 25 uvas puede haber uvas grandes y pequeñas y uvas verdes, uvas maduras y uvas podridas. Para contar una población humana en la que hay varones y mujeres podemos contar independientemente unos y otras, o bien abstraer dicha diferencia y contar «personas». De la misma manera, podremos contar cuántas «frutas» hay en un canasto en el que hay peras y manzanas, pero obviamente, como nos enseñaron en el colegio, no podemos sumar directamente peras con manzanas.

En las cantidades resultado de una medición la unidad elegida, que llamaré en adelante unidad métrica, es arbitraria y no viene dada, como en los recuentos, por la naturaleza concreta de lo que se quiere cuantificar. Así la distancia entre dos ciudades puede medirse en kilómetros, millas terrestres, millas marinas y, por qué no, también en pulgadas o años-luz. Pero sea cual sea la unidad métrica en la que damos una distancia, la dimensión de dicha magnitud es siempre la misma. Pero, ¿qué es una dimensión?

Cuando en el ámbito de las ciencias naturales básicas –la física y la química– se desarrolló la teoría de la medición hace ya un par de siglos, se creó un campo científico denominado análisis dimensional, que es el que se encarga de analizar las unidades y las dimensiones correspondientes a diversas magnitudes y cantidades. Un aspecto básico del análisis dimensional es que las cantidades que se usan en la ciencia y en la vida cotidiana son realmente productos matemáticos. Cuando decimos, por ejemplo, «30 metros», realmente estamos expresando el resultado de acumular 30 veces la unidad «metro». Así, 30 metros son realmente 30 x m, siendo «m» el símbolo de «metro». Igualmente, lo que en el habla habitual expresamos al decir «cuatro melocotones» matemáticamente se refiere al producto del número abstracto «4» por la unidad «melocotón» y si, por ejemplo, para hacer uso del alfabeto griego denominamos con la letra μ al melocotón abstracto, esos cuatro melocotones son 4 x μ (o, simplemente, 4 μ).

El análisis dimensional enseña que los recuentos tienen unidades, pero no dimensiones. Mientras que los recuentos son magnitudes adimensionales, las mediciones tienen tanto unidades como dimensiones.

Podríamos considerar la dimensión de una magnitud como aquello que resulta de abstraer las particularidades de todas las unidades en que puede medirse. Así la dimensión longitud sería lo que tienen en común el metro, la yarda, la pulgada, el año-luz, la versta rusa, el li chino, la milla terrestre, la milla marina... La dimensión tiempo es lo que tienen en común el milisegundo, el minuto, la semana, el siglo y el año-luz. Los físicos dicen que una magnitud es una propiedad física que se puede medir. Entonces, podemos concebir la dimensión de una magnitud como el aspecto común a todas las propiedades que se pueden medir en unidades similares (convertibles). La longitud de onda de una vibración sonora, las distancias interatómicas en una molécula, los diámetros de los orgánulos celulares o el espacio recorrido por un móvil en un segundo son todos ellos longitudes. Lo que tarda un péndulo en hacer su recorrido, el lapso que transcurre desde el orto hasta el ocaso, el periodo en que se desintegran la mitad de los átomos de una sustancia radiactiva... son todos ellos tiempos. En ciencias sociales el análisis dimensional está mucho menos desarrollado, pero podemos considerar que las cantidades en euros, yen japoneses, dólares estadounidenses o reales brasileños expresan todas ellas la dimensión dinero.

Dimensiones básicas y dimensiones derivadas

Las dimensiones de una magnitud se expresan mediante su fórmula dimensional, que es el producto de potencias de las cantidades o dimensiones fundamentales con las que se define una magnitud física. Aunque esta definición parece difícil de entender para los no versados en matemáticas, los ejemplos la aclararán.

Como las unidades de longitud, de masa y de tiempo expresan aspectos definidos, delimitados e irreducibles a otras magnitudes, los físicos comenzaron a considerar estas tres magnitudes o cantidades como magnitudes o cantidades fundamentales y para expresar la dimensión de cada una de ellas escogieron simplemente la letra inicial (generalmente mayúscula, aunque por ejemplo Emiliani usa minúsculas). Así la fórmula dimensional de la longitud es L, la de la masa, M y la del tiempo, T.

En cambio, las unidades en las que se expresan otras cantidades son claramente definibles como unidades derivadas de las unidades de longitud, masa o tiempo. Si para hallar la superficie de un rectángulo multiplicamos su base, 3 metros (es decir, 3 x m), por su altura, 7 metros (o sea, 7 x m), el resultado será (3 x m) x (7 x m). Y como el orden de los factores no altera el producto,

(3 x m) x (7 x m) = (3 x 7) x (m x m) = 21 x m²

es decir, 21 m². El ejemplo muestra cómo la unidad de superficie que denominamos «metro cuadrado» es simplemente el resultado de multiplicar un metro por sí mismo, es decir, elevarlo al cuadrado. Como sea cual sea la unidad en que se mide la longitud, al multiplicar esa unidad por sí misma para obtener una superficie obtendremos esa unidad al cuadrado, todas las superficies tendrán la dimensión L², ya que toda unidad desuperficie es una longitud elevada al cuadrado.

La velocidad se define como el resultado de dividir el espacio recorrido por el tiempo invertido en recorrerlo, de forma que, si un barco navega 40 millas en dos horas, su velocidad será:

Pero como la unidad resultante de dividir una milla por una hora o, dicho en términos coloquiales, la milla por hora, tiene un nombre especial, «nudo», se usa ese nombre especial y se dice así que el barco navega a una velocidad de 20 nudos.

El nudo es un caso particular, porque buena parte de las cantidades que se investigan en la ciencia se expresan en unidades derivadas que no tienen nombre especial y que se obtienen simplemente por división o multiplicación de unidades básicas. Así la velocidad suele expresarse en kilómetros (divididos) por hora (km/h) o en metros (divididos) por segundo (m/s). La fórmula dimensional de la velocidad es así L/T, o sea, longitud dividida por tiempo. Pero dividir una cosa por otra es lo mismo que multiplicar la primera por la inversa de la segunda, y la inversa de una cantidad puede expresarse como esa cantidad elevada a -1. Por lo tanto,

Eliminando el punto que indica el producto -como se hace casi siempre en álgebra superior-, la fórmula dimensional de la velocidad resulta LT y el tiempo elevado a -1.

La aceleración es el cambio de la velocidad por cada unidad de tiempo, de forma que si la velocidad disminuye 10 m/s cada 5 segundos, la aceleración es

Eso significa que en cada segundo, la velocidad disminuye 2 m/s, lo que se expresa diciendo que la aceleración es de –2 m/s², o bien –2 ms^-2. La lectura de expresiones como esta a menudo da lugar a ambigüedad, porque si, por ejemplo, leemos m/s² como «metro por segundo al cuadrado», sería posible interpretar que lo que queremos decir es (m∙s)² , es decir, m²∙s², o bien m∙s², o incluso (m/s)², es decir, m²/s². Todo esto es muy peligroso porque obviamente  (m∙s)²  no es lo mismo que (m/s)² (que equivale a m²/s²). En general, los físicos prefieren escribir esa unidad de aceleración como  m s^–2, y leen «metro segundo a la menos dos»,  expresión que, siendo muy poco elegante, resuelve en cambio las ambigüedades que introduce nuestra querida preposición «por». Por lo tanto, como la aceleración es siempre el resultado de dividir una velocidad por un tiempo, su fórmula dimensional es

(LT ^-1)/T = LT ^-1∙(1/T) = LT ^-2.

La fuerza se define en física como la masa multiplicada por la aceleración y, como la masa es magnitud fundamental con fórmula dimensional M, la fórmula dimensional de la fuerza es M·LT ^-2, es decir,MLT ^-2. Una de las unidades de fuerza más usadas es el producto de multiplicar el kg masa por la aceleración en m/s², o sea:

  kg ∙ m ∙ s ^–2

El resultado se denomina newton y se abrevia N. Por lo tanto, un newton es simplemente el resultado de multiplicar un kilogramo por un metro y dividirlo por un segundo cuadrado. Esto puede parecer extraño para quien piense que solo se pueden multiplicar números y que es absurdo multiplicar kilogramos por metros o excavadoras por horas. Sin embargo, gracias a esas multiplicaciones «absurdas» obtenemos unidades que nos permiten medir cantidades que son importantes a efectos prácticos.

Por ejemplo, supongamos que queremos comparar la cantidad de trabajo necesario para excavar dos túneles. En uno trabajaron 10 excavadoras, 200 horas cada una; en otro trabajaron 3 excavadoras durante 600 horas cada una. Si definimos la cantidad de trabajo como el producto del número de excavadoras por las horas trabajadas por cada excavadora, en el primer caso la cantidad de trabajo son 10 excavadoras x 200 horas, o sea, (10 x excavadora) x (200 x hora) = 2.000 excavadora x hora. En el segundo túnel el trabajo invertido fueron (3 x excavadora) x (600 x hora) = 1.800 excavadora x hora. De forma que, usando como unidad de trabajo la «excavadora multiplicada por » (unidad que presupone que la cantidad de trabajo invertida cuando una excavadora trabaja 10 horas es igual a la invertida cuando 10 excavadoras trabajan una hora), en el primer túnel se invirtieron 2.000 unidades de trabajo y en el segundo solamente 1.800. En un caso como este, lo habitual al referirse a esa cantidad de trabajo es decir que se gastaron tantas «horas-excavadora». Pero, como el producto de los factores no altera el producto, «excavadoras-hora» también parece admisible. En cambio, a pesar de que estamos hablando del producto de una excavadora por una hora, ni horas por excavadora(s) ni excavadoras por hora(s) son buenas denominaciones para esa unidad, como se verá.

Hemos visto pues que cualquier unidad de velocidad es una unidad de longitud dividida por una unidad de tiempo y aunque km/h es un kilómetro dividido por una hora, se lee generalmente «kilómetros por hora». De la misma manera, si en el banco nos cambian 35 libras esterlinas por 70 dólares estadounidenses, el tipo de cambio es (35£)/(70$), o sea, 2 $/£, lo que se leería generalmente «dos dólares por libra». Igualmente, la presión que ejerce un cilindro que pesa 100 kg sobre su base de 20 cm2 es (100 kg)/(20 cm²) = 5 kg/cm², lo que podría leerse por ejemplo como «cinco kilos por centímetro cuadrado». En general, las unidades derivadas que se forman dividiendo una unidad por otra, en castellano suelen leerse usando la preposición «por». Eso crea problemas cuando de lo que se trata es de una unidad derivada formada no por división, sino por multiplicación. Así, en electricidad una unidad de energía (o «trabajo», como dicen a menudo los físicos) muy utilizada es la que resulta de multiplicar un kilovatio (kW) por una hora (h). Si un calentador eléctrico tiene una potencia de 50 kW y lo mantenemos funcionando 3 horas, la energía consumida será 50 kW x 3 h = 150 kWxh. En términos matemáticos, kW xh (a veces escrito kW·h), expresa claramente que se trata del producto de un kilovatio por una hora, pero si decimos «kilovatio por hora», como se ve a veces, parece que se trata justamente de un kilovatio dividido por una hora (kW/h). Por eso lo mejor y lo más aceptado es decir o escribir «kilovatio-hora» para describir con palabras esa unidad de consumo eléctrico.

En general, en castellano las unidades derivadas formadas mediante división se nombran usando la preposición «por» y si se quiere formar el plural de dicha unidad, se hace el plural de la unidad que está en el numerador. Así g/cm², suele leerse gramo(s) por milímetro cuadrado; kg/m³ es kilogramo(s) por metro cúbico; la frecuencia cardíaca se expresa en un número de latidos (dividido) por minuto y la velocidad angular en radianes (divididos) por segundo. Por el contrario, para denominar las unidades derivadas formadas mediante multiplicación, simplemente se nombran las unidades una tras otra y generalmente se escriben unidas por un guión. Así, por ejemplo, kilovatios-hora (para expresar energía eléctrica), horas-trabajador (para expresar cantidad de trabajo), o toneladas-kilómetro (para expresar la cantidad de transporte que tuvo lugar durante un año). De todo lo anterior deduzco las reglas que enunciaré a continuación, que nunca he visto escritas, pero que creo responden a la práctica científico-técnica en nuestro medio lingüístico y sirven para evitar ambigüedades y errores. Son las siguientes:

1. En castellano las unidades derivadas formadas por la multiplicación de otras dos unidades deben nombrarse mediante aposición de las dos unidades que se multiplican. No es correcto en estos casos expresar el producto mediante la preposición «por».

2. Al escribir dichas unidades con el nombre completo, sin abreviar las unidades originarias, debe usarse un guión para enlazar las unidades integrantes.

3. Para hacer el plural de dicha unidad derivada basta hacer el plural de la primera unidad integrante del producto. Ejemplos: «kilovatio-hora». Plural: «kilovatios-hora». Formas incorrectas: «kilovatio por hora», «kilovatio hora».

En diversos campos de la ciencia a menudo se desea cuantificar la cantidad de observación a que se somete un grupo. Así, por ejemplo, en estudios comparativos de la eficacia de distintas terapéuticas, a menudo se usan unidades formadas multiplicando la unidad biológica observada por la unidad de tiempo pertinente. Así, si se observan personas tratadas con un fármaco para ver cuán a menudo ocurre cierto efecto adverso, la unidad puede ser por ejemplo la persona-día y así, si observamos a 10 personas durante una semana y a 4 personas durante 5 días, obtendremos un total de 90 (o sea, 10 x 7 + 4 x 5 = 70 + 20) unidades de observación que podemos denominar personas-día o días-persona, indistintamente. También podríamos usar como unidad de tiempo la semana y entonces tendríamos 90/7 = 12,86 (aproximadamente 13) semanas-persona o personas-semana de observación. Ahora bien, tanto el día como la semana son unidades métricas, de tiempo (por eso podemos usar decimales), mientras que las personas son unidades de recuento (no podemos tener 0,3 personas) y, por tanto, parece preferible decir semanas-persona en vez de personas-semana. Igualmente, para determinar la probabilidad de accidente en una central nuclear por año de funcionamiento, puede dividirse el total de accidentes observados por el total de años de observación de centrales en funcionamiento. En el denominador habrá que poner, pues, una cantidad cuyas unidades son los «años-central» (mejor que «centrales-año»). El total de transporte de contenedores en un país puede cuantificarse, por ejemplo, en kilómetros-contenedor (mejor que «contenedores-kilómetro»). En estos casos el supuesto que se hace es que una persona observada durante x horas produce igual cantidad de observación que x personas observadas durante una hora e, igualmente, n centrales nucleares observadas durante un año generarán una cantidad de observación equivalente a la obtenida de una sola central observada n años (estas equivalencias son tanto menos creíbles a medida que los plazos considerados se diferencian más). En el caso de la cantidad de transporte, el de 500 contenedores transportados cada uno un kilómetro se considera equivalente al de un solo contenedor transportado 500 km.

Si se observa la lógica de la formación de las unidades derivadas en estos casos, se puede deducir una cuarta regla que habría que añadir a las tres anteriores:

4. Cuando la unidad derivada está formada por el producto de una unidad métrica (una unidad de medida propiamente dicha) y una unidad de recuento, la unidad métrica debe anteponerse a la unidad de recuento y el plural se formará pluralizando solamente la unidad métrica. Ejemplos: horas-trabajador (para medir la cantidad de trabajo insumido), kilómetros-pasajero (para cuantificar el transporte de personas en una red ferroviaria), horas-espectador (para cuantificar el consumo de espectáculos deportivos), meses-mujer (para cuantificar el uso de píldoras anticonceptivas).

Una persona familiarizada con estos conceptos que en un texto referido a un estudio de supervivencia de cáncer de mama encuentre la expresión pooled person-time added up to 988.0 woman-years producirá de una forma perfectamente lógica una traducción tal como «el total acumulado de personas-tiempo fue de 988,0 años-mujer». Obviamente, «el total acumulado de tiempo-personas...» también sería una traducción adecuada de pooled person-time.

Como los recuentos no tienen dimensiones, la fórmula dimensional de una cantidad de observación medida en horas-persona y una cantidad de transporte medida en horas-pasajero es exactamente la misma, T. Estas cantidades tienen como única dimensión el tiempo. Pero eso no significa que tengan las mismas unidades, como a veces se arguye incorrectamente.

Números adimensionales y sin unidades

El análisis dimensional enseña también que hay magnitudes que no tienen ni dimensiones ni unidades (en inglés, unitless numbers). Tomados como tales, números reales como el número π (cuyo valor aproximado es 3,1416...), el número e (= 2,7183...) o la raíz cuadrada positiva de 16 que, como sabemos es 4, son entes sin dimensiones y sin unidades. Pero, ¿por qué es π adimensional, por qué no tiene unidades intrínsecas? De la escuela secundaria debemos recordar que la longitud L de una circunferencia es L = 2πr, lo que significa que para calcular la longitud de la circunferencia multiplicamos el número π por el doble del radio, es decir, por el diámetro. De forma que, llamando d al diámetro, L = πd. Si despejamos π de esta fórmula, resulta π = L/d, que significa exactamente que si dividimos la longitud de una circunferencia por el doble de su radio —es decir, su diámetro— obtenemos π. Los matemáticos de la antigüedad descubrieron que el cociente entre la longitud de una circunferencia y su diámetro es un número constante y ese número es lo que llamamos π. Si, por ejemplo, medimos la circunferencia en pulgadas y el diámetro en pulgadas, al dividir una por el otro resultará algo así como:

 = π

El resultado de dividir cualquier cosa por sí misma es el número adimensional 1, por lo tanto el resultado x/y no tiene unidades, es adimensional. Igualmente son adimensionales y sin unidades todas las magnitudes resultado de dividir una magnitud por otra magnitud similar. Si 7,9% expresa el desempleo en una región como tanto por ciento de desempleados respecto de la población económicamente activa (PEA), 7,9%, que es lo mismo que 7,9/100, o sea 0,079, es el resultado de dividir un número de personas (los desempleados) por otro número de personas, la PEA. Por ello es un número adimensional y sin unidades. Cualquier cociente entre dos cantidades expresadas en las mismas unidades es un número sin unidades y adimensional.

El análisis dimensional ayuda a hacer cómputos sin cometer errores en las unidades. Supongamos por ejemplo que una libra esterlina (1£) se cambia en el mercado de divisas por un dólar con ochenta y cinco centavos de dólar (1,85$). Entonces 1£=1,85$ y si llamamos t_£/$ al tipo de cambio de libras esterlinas a dólares, y t_£/$ = 1,85$/£, el tipo de cambio de dólares a libras será t_$/£ = 1£/1,85$, es decir, t_$/£ = 0,54£/$. Al multiplicar una cantidad en libras por el tipo de cambio de libras a dólares obtenemos la cantidad en dólares, como puede comprobarse: 20£ x 1,85$/£ = (20 x 1,85) x (£ x $/£). Como en el segundo paréntesis la libra esterlina está tanto multiplicando como dividiendo, se elimina del numerador y del denominador y el resultado son 37$.

De formalismos matemáticos y de cómo leer expresiones algebraicas

En aritmética nos enseñaron que la multiplicación se expresa con el aspa (x) o con el punto elevado (·) cuando se trata de números (3 x 4 = 3 · 4 = 12) y se lee mediante la preposición «por» (tres multiplicado por cuatro o, simplemente, tres por cuatro, doce). La división se expresa mediante los dos puntos (:) o la barra de quebrado (/) y, como vimos, en la práctica se lee unas veces con la preposición entre y otras con la preposición por (7:3 = 7/3 se lee «siete (dividido) entre tres» o «siete dividido por tres»). Sin embargo, como ya hemos visto, cuando la división no se refiere a números sino a unidades, prácticamente siempre se lee con la preposición por, así metro por segundo (m/s), kilómetro por hora (km/h), amperio por segundo (A/s).

La matemática se basa en un lenguaje escrito altamente formalizado, repleto de normas que evitan la ambigüedad, mientras que el habla está llena de posibilidades de ambigüedad y polisemia. Si, por ejemplo, alguien dice «pi más equis al cuadrado», no queda claro si a lo que se refiere es a

π + x²

o bien a

(π + x)²

Mientras que la expresión «pi más equis al cuadrado» contiene 20 caracteres tipográficos y es una expresión ambigua, cualquiera de las dos expresiones algebraicas anteriores (que contienen respectivamente 4 y 6 caracteres tipográficos) es absolutamente precisa. Además, las expresiones algebraicas son comunes a todos los idiomas y probablemente cualquier persona culta, sea brasileña, rusa o canadiense, entiende lo que significa

(π + x)²

y sabe también que πr² representa el área de un círculo de radio r. Por el contrario, cuando estas expresiones se ponen en palabras, cada idioma generará su propia lectura y se habrá acabado la posibilidad de comprensión mutua.

En otros tiempos los polinomios y los monomios se enseñaban en el álgebra de la enseñanza secundaria. Ignoro si esas cosas se siguen enseñando en España y en otros países. Lamentablemente, en EE.UU. muchos estudiantes llegan a la universidad sin saber casi nada de ellas. Pero no nos vayamos por las ramas y recordemos que un polinomio es una expresión algebraica como π + x² o como 8x³ – 9x²– 4x + 5, en la que varios monomios están unidos por la adición o suma (la substracción es la suma de un elemento con signo menos). En cada monomio solamente hay coeficientes numéricos y variables unidos por productos. Así 8x³ es realmente el producto 8·x·x·x. También es un polinomio la expresión ax²– bx en la que a y b son coeficientes de valor desconocido. Como en ax²– bx hay solamente dos monomios, este polinomio se denomina binomio.

Para leer un polinomio se lee cada uno de los monomios que lo integran, intercalando los «más» o «menos» que los unen. Como el monomio ax² representa el producto del coeficiente a por el valor de x elevado al cuadrado, para leerlo podríamos decir por ejemplo «a multiplicado por equis elevado al cuadrado». Sin embargo, hay mucha palabrería en eso y los matemáticos hacen mucho énfasis en la concisión. Así, a pesar de que las fórmulas matemáticas están llenas de productos, casi siempre se obvian los signos de multiplicación, aunque a veces —raramente— se usa el punto elevado (·). El producto de dos variables x e y puede verse escrito alguna vez como x·y, pero lo habitual es escribir simplemente xy. El aspa (x) con el que se representa la multiplicación en aritmética no suele usarse nunca en álgebra para indicar el producto, por la muy posible confusión de ese símbolo con la letra x que tanto se utiliza para indicar una variable. Y si se obvia el signo para indicar la multiplicación, casi siempre se obvia también la indicación verbal (el«por») para indicar el producto. Muy raro será oír a alguien versado en matemáticas leer πx como «pi por equis», o 3z como «tres por zeta». Lo habitual será «pi equis» o «tres zeta».

Pero volvamos a la lectura de ax². El exponente 2 indica que la x está elevada al cuadrado y por ello se puede leer ese monomio «a por equis elevado al cuadrado» como antes se dijo, pero como lo habitual es suprimir el «por» alguien podría pensar que esto se podría leer «a equis elevado al cuadrado». Lo malo de tal expresión es que puede entenderse como el producto ax elevado al cuadrado, es decir (ax)² lo que es igual a a²x². Y, ciertamente, ax²  no es igual a a²x².

Para evitar ese problema, al leer algo como a²x² lo habitual es eliminar también todos los «elevado al» y seguir la convención matemática de expresar las potenciaciones leyendo el exponente 2 como «cuadrado» y el exponente 3 como «cubo». De esta manera, a²x² es simplemente«a cuadrado equis cuadrado»  y 6z³ es «seis zeta cubo».

Los matemáticos se fijan sobre todo en sus fórmulas escritas y dan poco valor a cómo se leen dichas fórmulas, ya que lo importante es lo que está escrito. Por ello una misma expresión matemática será leída unas veces de una manera y otras de otra, ya que hay considerable laxitud en cuanto a la lectura de las fórmulas matemáticas, particularmente cuando hay paréntesis, fracciones, etc., en cuyo caso el dictado de una fórmula se aditamenta con todas las cláusulas necesarias para que la fórmula se escriba de la forma correcta. Un caso donde hay mucha ambigüedad es el de los exponentes de potencias más allá del cubo, que en general se leen como «a la cuarta», «a la quinta», etc., pero no es raro oír dichos exponentes leídos directamente. Un monomio como a⁴x² se leerá muchas veces como «a cuatro equis dos» y todos lo entenderán, igual que se entenderá también a quien lo lea —con mucha más verbosidad— como «a (a la) cuarta (por) equis (al) cuadrado», o todas las variantes resultantes de eliminar una, varias o todas las partículas puestas entre paréntesis en la expresión anterior.

Como las expresiones algebraicas que más se usan son los polinomios de primero, segundo o tercer grado (es decir, con la variable elevada a la primera, segunda, o tercera potencia), la jerga desarrollada por los matemáticos para leer esos polinomios está más formalizada. Por lo general, al leer uno de esos polinomios se omiten todas las indicaciones de multiplicación y todos los «elevado a», el exponente 3 se lee «cubo» y el exponente 2 se lee «cuadrado». Así, por ejemplo, lo habitual es que    a²x³ – bx² se lea simplemente «a cuadrado equis cubo menos be equis cuadrado». Igualmente la fórmula que da la longitud del círculo, 2πr, se lee generalmente «dos pi erre» y su área, πr², «pi erre cuadrado», mientras que el volumen de una esfera,

πr³

es «cuatro tercios de pi erre cubo».

Lo imprecisa que es la lectura de las ecuaciones matemáticas puede desconcertar a la gente «de letras», pero tiene poca importancia para los matemáticos, que saben que lo importante, que es lo que está escrito, no es ambiguo. En cambio, como las expresiones matemáticas son —si están bien escritas— totalmente precisas, ya que existen convenciones que eliminan cualquier ambigüedad, los que no están muy versados en dichas expresiones a veces creen escribir una cosa cuando están escribiendo otra.

Así, la mitad de la suma de dos números a y b puede escribirse

pero, si la barra horizontal de la fracción se cambia a barra oblicua y se escribe a + b/2, lo que se está indicando es siempre la suma de a con la mitad de b, o sea:

Para expresar la mitad de la suma a + b usando la barra oblicua de fracción hay varias posibilidades, como escribir  (a+b)/2, o bien ½ (a+b), o incluso a/2 + b/2. Pero a+b/2 (a no ser que a sea cero), no es lo mismo que

.

¿Metro al cubo o metro cúbico? ¿Ji al cuadrado o ji cuadrado?

Toda persona culta sabe que en castellano la expresión m² se lee «metro cuadrado» y m³ se lee «metro cúbico». Pero según las nociones de análisis dimensional expuestas anteriormente el metro cúbico es una unidad de volumen con dimensión L³, es decir, consecuencia de multiplicar una longitud por sí misma tres veces, de la misma forma que el metro cuadrado es una unidad de superficie con dimensión L². Esto significa que, en efecto, «metro cúbico» y «metro al cubo» son exactamente lo mismo, igual que son exactamente lo mismo «metro cuadrado» y «metro al cuadrado». Que se diga que la superficie de un espejo es «un metro cuadrado» y que casi nunca digamos que es «un metro al cuadrado» no significa que esta última expresión sea incorrecta desde el punto de vista matemático.

Sin embargo, hay quienes mantienen que el exponente 2 se lee como «cuadrado» cuando afecta a una unidad de medida, pero que ha de leerse «al cuadrado» cuando afecta a cifras o a letras. Esto no es correcto pues, como hemos visto, expresiones como «equis cuadrado» (x²) o «erre cuadrado» (r²) son de uso muy frecuente en matemáticas y de ninguna manera deben considerarse incorrectas.

La expresión χ² es muy frecuente por referirse a una prueba estadística a la que se alude en inglés con chi square unas veces, con chi squared otras (y a veces uniendo ambos términos con un guión en chi-squared test). Dicha expresión puede traducirse correctamente al castellano como «ji cuadrado» o «ji al cuadrado». Hay quienes mantienen que «ji cuadrado» es una expresión incorrecta, opinión que a mi juicio no tiene fundamento ni matemático ni gramatical. De hecho, para la gente versada en matemáticas «ji cuadrado» es más breve que «ji al cuadrado» y, por tanto, preferible. Por lo demás, quizá no esté de más decir aquí que desde hace siglos la letra griega χ se llama chi en inglés (pronunciado «cai», no «chi») y «ji» en castellano. Por ello los que hablan en español de «la prueba de chi cuadrado» (o, peor, del «test de chi cuadrado») revelan que están expresándose en espanglish, probablemente sin saberlo. En eso Navarro y Silva sí que llevan toda la razón.

Bibliografía

Daintith, J. / R. D. Nelson eds. (1989) The Penguin Dictionary of Mathematics, Penguin, London

De Jong, F. (1967) Dimensional Analysis for Economists, North Holland, Amsterdam

Emiliani, C. (1987) Dictionary of the Physical Sciences —Terms, Formulas, Data, Oxford University Press, New York

Frey, G. (1972) La matematización de nuestro universo, trad. de J. Barrio / G. del Toro, Madrid

Gómez Díaz, R. (2002) «Traducir los números», 10-24 en Puntoycoma 78

Huntley, H. E. (1951) Dimensional Analysis, Rinehart, New York

Jupp, E. W. (1962) An Introduction to Dimensional Method, Cleaver-Hume, London

Kleiber, J. / J. Estalella (1938) Compendio de física y química, Gustavo Gili, Barcelona

Mosterín, J. (1978) «La estructura de los conceptos científicos»,82-93 en Investigación y ciencia 16

Navarro, F. (2000) Diccionario crítico de dudas inglés-español de medicina, McGraw-Hill, Madrid [p. 87, entrada chi-squared]

Palacios, J. (1964) Dimensional Analysis [ed. orig. 1956, Análisis dimensional, Espasa-Calpe, Madrid], trad. de P. Lee / L.Roth, Macmillan, London

Parker, S. P. (1985) The McGraw-Hill Dictionary of Physics, McGraw-Hill, New York

Paulos, J. A. (1988) Innumeracy —Mathematical Illiteracy and its Consequences, Hill & Wang, New York

Silva, G. A. (1990) «Las incorreccciones del chi cuadrado»,116 en Medicina Clínica 95

Staicu, C. I. (1982) Restricted and General Dimensional Analysis, Abacus Press, Turnbridge Wells, Kent

Tapia Granados, J. A. / F. J. Nieto (1994) «A propósito de la versión española del Diccionario de epidemiología de J. M. Last», 94-98 en Gaceta Sanitaria 8

Tapia Granados, J. A. (2001) «La estadística y el castellano: la terminología estadística en la nueva edición del Diccionario de uso del español», en Nómadas - Revista Crítica de Ciencias Sociales y Jurídicas 3

José A. Tapia Granados
Universidad de Michigan
Ann Arbor, Michigan, EE. UU.
jatapia@umich.edu